Voir la page en français

A link between online changepoint and geometry for big data

Leveraging a link between online changepoint detection and computational geometry for big data analysis

In recent years, many methods have been proposed for detecting changepoints in big datasets. The reason for such a keen interest in changepointdetection methods lies in its importance for various real-world applications, including bioinformatics and genomics (e.g., DiffSegR  published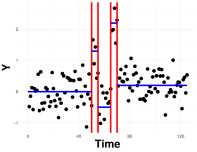

Figure 1. A stream with 4 red changes in the blue mean
Figure 1. A stream with 4 red changes in the blue mean
by the GNet and OGE team), medicine, finance, or biology (neuroscience, plant sciences…).he challenge is to detect and locate changes in the distributionofthe data over time. 

. Figure 1 illustrates a data-stream with 4 changes in the mean, but there are more intricate applications, e.g. changes in the variance or network structure. As technology develops, the demand for changepoint procedures capable of processing massive datasets in real-time (online) has increased.

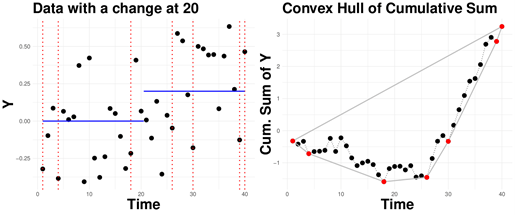
With colleagues from Evry University and Lancaster University, UK (L. Pishchagina, G. Romano, P. Fearnhead and V. Runge), G. Rigaill from the GNet team at IPS2 established a connection between the detection of a single changepoint in p-dimensional data streams and geometry, in an article published in the Journal of the Royal Statistical Society - Series B. They propose an algorithm that exactly computes the likelihood-ratio test for a single changepoint in p-dimensional data streams, based on this connection. The algorithm is straightforward, apparently quasi-linear, and fast: for one million data points with p = 3, it runs in about two minutes.

The algorithm is general in that it can be used for a wide range of models from the exponential family, including multivariate data where:

1.      the parameters prior to the change are unknown ;

2.      different streams are modeled by different distributions.

The authors additionally :

1.      provide statistical guarantees on the probability of false alarms and the detection delay ;

1.      derive variants for sparse and high-dimensional settings ;

2.      show that the algorithms are fast and accurate in practice using simulation and NBA (National Basketball Association, USA) data.

Figure 2. For a single change in a univariate data-stream Yi, the connection states that only the vertical changes red dotted lines (on the left), corresponding to the red dots on the hull of the cumulative sum of the data (t, Σt Yi; on the right), can optimize the fit to the data.
Figure 2. For a single change in a univariate data-stream Yi, the connection states that only the vertical changes red dotted lines (on the left), corresponding to the red dots on the hull of the cumulative sum of the data (t, Σt Yi; on the right), can optimize the fit to the data.

23/09/2025