Détection de ruptures en ligne et géométrie dans les analyses de « big data »

Un lien entre la détection de ruptures en ligne et la géométrie computationnelle pour les analyses de « big data »

Ces dernières années, de nombreuses méthodes ont été proposées pour détecter des ruptures dans les jeux de données à grande échelle.

Figure 1. Des données avec 4 ruptures rouges dans la moyenne bleue

L'intérêt pour ces méthodes s'explique par leur importance pour diverses applications issues du « monde réel », notamment la bioinformatique et la génomique (e.g. DiffSegR, publié par les équipes GNet et OGE), la médecine, la finance, ou la biologie (neuroscience, science des plantes…).

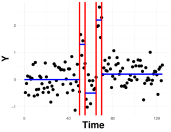
Le défi consiste à détecter des ruptures dans la distribution des données au cours du temps. La figure 1 illustre des données avec 4 ruptures dans la moyenne, mais il existe des applications plus complexes, par exemple pour détecter des ruptures dans la variance ou de la structure d'un réseau. Avec les progrès technologiques, la demande de procédures capables de traiter des jeux de données massifs en temps réel (en ligne) a augmenté

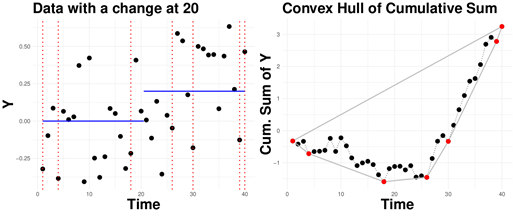
Avec des collègues de l’université d’Évry Paris‑Saclay et de Lancaster (L. Pishchagina, G. Romano, P. Fearnhead et V. Runge), G. Rigaill de l’équipe GNet à IPS2 a établi, dans un article publié dans le Journal of the Royal Statistical Society, Series B, un lien entre la détection de ruptures dans des données p‑dimensionnelles et la géométrie. Ils proposent un algorithme qui calcule exactement le test du rapport de vraisemblance pour une rupture dans des données p‑dimensionnelles, basé sur ce lien. L’algorithme est simple, apparemment quasi‑linéaire, et rapide : pour un million de points et p = 3, il s’exécute en environ deux minutes.

L’algorithme est général au sens où il peut être utilisé pour une grande variété de modèles de la famille exponentielle, y compris des données multivariées où :

1. les paramètres avant la rupture sont inconnus;

2. les différentes dimensions sont modélisées par des distributions différentes.

Les auteurs montrent aussi que les algorithmes permettent :

1. de fournir des garanties statistiques sur la probabilité de fausses alertes et le délai de détection;

2. de dériver des variantes pour les cas parcimonieux et en haute dimension;

3. d’analyser les données rapidement et efficacement sur des cas pratiques à l’aide de simulations et de données de la NBA (« National Basketball Association », USA).

Figure 2. Pour une unique rupture dans des données univariées Yi, le lien établit que seules les ruptures verticales en pointillés rouges (à gauche), correspondant aux points rouges sur l'enveloppe convexe de la somme cumulée des données (t, Σt Yi; à droite), peuvent optimiser l'ajustement aux données.

23/09/2025